计算几何读书笔记

第一次接触到计算几何，非常有意思。

Bookmark

CGAA: Computational Geometry Algorithms and Applications 3rd

Line Segment Intersection

2018.6.22, CGAA

问题. 给定一个大小为$n$的平面线段集合，其中每条线段由两个端点确定，求其中所有线段间的交点。

两条线段是否相交可以$\mathrm{O}(1)$确定，于是遍历所有无序线段对给出了$\Theta (n^2)$的暴力算法，这显然太naive了。容易观察到，线段$s_i$和$s_j$相交的一个必要条件是它们在$y$轴（或者任意一个轴）上的投影存在重叠部分，于是我们可以给出以下改良：初始时所有线段的标记均为out，用一根sweep line从上往下扫描，每当遇到一条线段的entry point，就把该线段标记为in并测试它和所有其他处于in状态的相交性；每当遇到一条线段的exit point，就将其标记改回out。这一算法规避了在$y$轴上投影不重叠的线段间的相交测试。但是在$y$轴上投影重叠的两条线段可能在其他轴上相距很远，该算法在最坏情况下还是$\Theta (n^2)$的。

进一步的改进基于以下观察：假设所有和sweep line相交的线段按交点的$x$坐标排序，则每条线段只需要和左右相邻的两条线段进行相交测试。

在算法运行之初，所有线段都和sweep line不相交，因此这些线段两两“不相邻”。在sweep line向下运动的过程中，什么时候两条线段会变得相邻，从而需要进行相交测试呢？有以下几种情况——

1. Entry事件：遇到某条线段$s_j$的entry point时，设此时和sweep line相交的线段按排序为$\dots ,s_i,s_j,s_k,\dots$，则$s_j$变得和$s_i$以及$s_k$相邻。

2. Exit事件：遇到某条线段$s_j$的exit point时，若原来和sweep line相交的线段排序为$\dots ,s_i,s_j,s_k,\dots$，则$s_i$和$s_k$变为相邻。

3. 交点事件：遇到两条线段$s_i$和$s_j$的交点时，若原来和sweep line相交的线段排序为$\dots ,s_h,s_i,s_j,s_k,\dots$，则$s_h$和$s_j$变为相邻，$s_i$和$s_k$变为相邻。

基于此，只需从上往下地移动sweep line，每次遇到这种“变得相邻”的事件，就对当事的两条线段进行相交测试即可。Entry point和exit point事件都非常容易探测，而对于交点事件，我们有这样的结论：在sweep line移动到$s_i$和$s_j$的交点$p$之前，$s_i$和$s_j$一定已经经历过相交测试，即$p$一定已经被发现过了。这样一来，我们就可以保证不漏过任何一个“变得相邻”事件，从而找出所有的线段交点。

该算法时间复杂度为$\mathrm{O}((n+k)\log n)$，其中$n$为线段数量，$k$为交点数量——建立和维护有序结构（比如使用红黑树）使得每次基本操作（插入删除查询等）是$\mathrm{O}(\log n)$的，而事件总数（entry+exit+intersect）则是$\mathrm{O}(n+k)$的。

注意这里没有叙述对一些微妙corner case的处理，比如如何handle水平线段、如何应对多条线段交于一点的情况等，它们并不会影响算法的时空复杂度，但实现的时候需要仔细处理。

Doubly-Connected Edge List

2018.6.22, CGAA

考虑平面的一个联通子集上的区域划分，设区域边界都是直线，于是每个区域都是一个多边形。Doubly-Connected Edge List（DCEL）是用以表示该划分的一种数据结构，它支持以下操作：

1. 遍历某个面的所有边
2. 遍历通过某个顶点的所有边
3. 通过一个面的某条边访问占据该边的另一个面

DCEL大概长这样：

struct vertex_t;
struct fce_t;
struct half_edge_t
{
    half_edge_t *succ, *prev, *twin;
    vertex_t *origin;
    face_t *face;
};
struct vertex_t
{
    point2f coord;
    half_edge_t *edge;     // arbitrary edge that has the vertex as its origin
};
struct face_t
{
    half_edge_t *edge;     // arbitrary edge of its outer boundary
    list<edge*> int_edges; // one for each hole in the interior
};

每条边被拆分为两条“half edge”，合称为一个“twin”。每个面由一系列half edge围起来，并且约定每条half edge的face位于它的左边（这保证了edge方向的一致性）。每条half edge都记录着它在自身所处的逆时针环中的前驱和后继，这构成一个循环链表。此外，half edge中还记录着其twin中的另一条half edge，以及自身的起点。

其实这个结构挺trivial的，很容易根据定义想到上面列举的三种操作该如何实现。

Art Gallery Theorem

2018.6.22, CGAA

Simple Polygon: regions enclosed by a single closed polygonal chain that does not intersect itself.

Diagonal: an open segment that connects two vertices and lies in the interior of the polygon.

Triangulation (of polygon): a decomposition into triangles by a maximal set of non-intersecting diagonals.

通过对多边形顶点数$n$做归纳，容易证明：

Theorem. Every simple polygon admits a triangulation, and any triangulation of a simple polygon with $n$ vertices consists of exactly $n-2$ triangles.

也就是说，线性输出规模的三角化对简单多边形总是可行的。在此基础上，容易证明三角化后的简单多边形的对偶图是一棵树，于是可以用线性时间对三角化的结果进行3着色，并得到以下推论：

Art Gallery Theorem. For a simple polygon with $n$ vertices, $\lfloor n/3\rfloor$ cameras are occasionally necessary and always sufficient to have every point in the polygon visible from at least one of the cameras.

Overlay of Two Subdivisions

2018.6.23, CGAA

给定两个平面上的subdivision ${\mathcal{S}}_1,{\mathcal{S}}_2$，定义它们的overlay $\mathcal{O}({\mathcal{S}}_1,{\mathcal{S}}_2)$为：面$f\in \mathcal{O}({\mathcal{S}}_1,{\mathcal{S}}_2)$当且仅当存在$f_1\in {\mathcal{S}}_1,f_2\in {\mathcal{S}}_2$使得$f$是$f_1\cap f_2$的某个极大联通子集。

$\mathcal{O}({\mathcal{S}}_1,{\mathcal{S}}_2)$的计算方法和所使用的subdivision表示方法息息相关，在这里假设是输入输出都用DCEL表示。容易证明两个输入DCEL中没有发生相交的那些half edge、face和vertex都可以原封不动地拷贝到输出DCEL中，需要重新计算的仅仅是${\mathcal{S}}_1$和${\mathcal{S}}_2$之间发生了相交的部分。

考虑之前提到的全局线段求交算法，我们把两个DCEL中的edge临时视为closed segment，然后用求交算法求全局交点。在sweep line往下扫的时候，根据遇到的event point类型来修正DCEL的vertex和edge信息是不困难的，不过需要非常多的分类讨论。这个过程只需要保证一个invariant：在任意时刻sweep line上方的DCEL的vertex和edge是正确的。

比较麻烦的是新face的计算，我们需要确定有哪些新face记录要添加，为遭遇变动的face更正edge指针，修改变动的face的edge中的face指针，以及为新face根据原face的label name赋予正确的label值。

在之前的步骤中，已经计算了顶点和边的信息。每条half edge都处于唯一的一个循环链表中，这个edge half list称为一个“boundary”。给定一个boundary，如何判定它是一个face的外边界还是内部的hole的轮廓呢？这可以通过boundary中的lowest leftmost vertex的两条相邻edge间的转角结合“boundary中边的左边是它所处的face”的约定来实现。

另外，由于face需要持有它所有boundary入口的链表，我们还需要判定哪些boundaries隶属于同一face。为此，考虑图$\mathcal{G}$：

1. 每个boundary对应$\mathcal{G}$中的一个顶点，此外对subdivision最外面的那个unbounded “face”，也设置一个对应的顶点。
2. 对两个boundaries，若其中一个是boundary of a hole，而另一个boundary中恰有half edge是hole boundary的lowest leftmost vertex左方最近的一条边，则这两个boundary对应的顶点间有一条边。若某个boundary地lowest leftmost vertex左侧没有half edge，它就和unbounded face对应地节点链在一起。

Lemma. $\mathcal{G}$中的每个连通分量恰对应一个face的boundary集合。

乍一看，图$\mathcal{G}$的边集构造简直坑爹，但我们其实可以在sweep line扫描的过程中得到需要的信息——在每个event point处，很容易获得它左侧最近的边是哪条。

这个算法时间复杂度还是$\mathrm{O}((n+k)\log n)$，其中$n$是${\mathcal{S}}_1,{\mathcal{S}}_2$的复杂度之和。尽管算法的每一步都透露出trivial的气息，但是综合到一起颇有一种蒸汽朋克式的美感——也就是说，实现起来会很蛋疼。

最后，基于这个算法，二维矢量多边形的布尔运算可以很容易地实现，算是回答了我一直有些好奇的问题吧。

Polygon Triangulation

2018.6.23, CGAA

Polygon into Monotone Pieces

Monotone: a simple polygon is called monotone with respect to a line $\ell$ if for any line ${\ell }^{\prime }$ perpecdicular to $\ell$ the intersection of the polygon with ${\ell }^{\prime }$ is connected. A polygon that is monotone with respect to the $y$-axis is called $y$-monotone.

将多边形先转换为$y$-monotone pieces，能极大地简化将多边形三角化的过程。

Turn Vertex: 相邻的两条边都朝下或者都朝上的顶点称为turn vertex。把多边形转为monotone的过程也正是去除turn vertex的过程。

Below & Above: a point $p$ is below another point $q$ iff $(p_y<q_y)$ or $(p_y=q_y\wedge p_x>q_x)$. A point $p$ is above another point $q$ iff $(p_y>q_y)$ or $(p_y=q_y\wedge p_x<q_x)$。也就是说先按$y$坐标从下到上排序，对$y$相同的点再按$x$坐标从右往左排序，“左上”的点是最“高”的。

Start Vertex: a vertex $v$ is a start vertex iff its neighbors lie below it and the interior angle at $v$ is less that $\pi$.

Split Vertex: a vertex $v$ is a split vertex iff its neighbors lie below it and the interior angle at $v$ is greater than $\pi$.

End Vertex: a vertex $v$ is an end vertex iff its neighbors lie above it and the interior angle at $v$ is less than $\pi$.

Merge Vertex: a vertex $v$ is a merge vertex iff its neighbors lie above it and the interior angle at $v$ is greater than $\pi$.

其他的顶点就是常规顶点（regular vertex）了。

Lemma. a polygon is $y$-monotone if it has no split vertices or merge vertices.

这个算法依然是基于sweep line的，也就是拿一条平行于$x$轴的直线从上往下扫过待分割的多边形$\mathcal{P}$，$\mathcal{P}$的顶点集合就是所有的event point。现假设$v_1,\dots ,v_n$为$\mathcal{P}$所有顶点的一个逆时针排列，$e_1=\overline{v_1{v}_2},\dots ,e_n=\overline{v_n{v}_1}$是多边形的边集，我们的目的是用适当的diagonals干掉所有的split vertex和merge vertex。

Helper: 对某条边$e_j$，定义$\mathrm{helper}(e_j)$为

$$\arg \underset{v_y}{\min }\{v\mid {\ell }_y<v_y\le \mathrm{up}(e_j),\mathrm{HorSeg}(v,e_j)\text{ in }\mathcal{P}\}$$

即$y$介于sweep line和$e_j$的上端点之间的、到$e_j$的水平线段完全位于$\mathcal{P}$中的顶点中最低的那个。显然，把split vertex连到它左侧最近边的helper顶点就能干掉这个split。

Merge vertex的处理要更困难一些，因为它连接的对象是在sweep line的下方，即相关顶点的选择必须被推迟。设$e_j$是merge vertex $v_i$左侧最近边，则当sweep line扫描到$v_i$时，$v_i$必然成为$e_j$的helper顶点。在之后的扫描中，如果再次更新了$e_j$的helper，那么把$v_i$和$e_j$的新helper连接起来即可；否则，可以把$v_i$和$e_j$的下端点连接起来。所以，只需要每次更新某条边的helper或遇到某条边的下端点时，检查该边原本的helper是否时一个merge vertex即可。

如何找一个顶点的左侧最近边就不记了，sweep line的拿手好戏。于是乎，把简单多边形剖分成$y$-monotone多边形的算法就出炉了：

proedure make_polygon_into_monotone(P)
    for each vertex v[i] in P, ordered by desc y coord
        handle(v[i])

procedure handle_start_vertex(v[i])
    helper(e[i]) = v[i]

procedure handle_end_vertex(v[i])
    if(helper(e[i-1]) is a merge vertex)
        connect(helper(e[i-1]), v[i])

procedure handle_split_vertex(v[i])
    let e[j] = DirectLeft(v[i])
    connect(helper(e[j]), v[i])
    helper(e[j]) = v[i]
    helper(e[i]) = v[i]

procedure handle_merge_vertex(v[i])
    if(helper(e[i-1]) is a merge vertex)
        connect(helper(e[i-1]), v[i])
    let e[j] = DirectLeft(v[i])
    if(helper(e[j]) is a merge vertex)
        connect(helper(e[j]), v[i])
    helper(e[j]) = v[i]

procedure handle_regular_vertex(v[i])
    if the interior of P lies to the right of v[i]
        if(helper(e[i-1]) is a merge vertex)
            connect(helper(e[i-1]), v[i])
        helper(e[i]) = v[i]
    else
        let e[j] = DirectLeft(v[i])
        if(helper(e[j]) is a merge vertex)
            connect(helper(e[j]), v[i])
        helper(e[j]) = v[i]

好优美的算法……

Theorem. a simple polygon with $n$ vertices can be partitioned into $y$-monotone polygons in $\mathrm{O}(n\log n)$ time with an algorithm that uses $\mathrm{O}(n)$ storage.

Triangulating a Monotone Polygon

没什么好说的，一个把杂乱的思路理得非常清楚，但又似乎很trivial的算法：

把P的顶点分为左链和右链，并把所有顶点从上到下排序，记排序结果为u[1..n]
procedure triangulate_monotone_polygon(u)
    stack.clear()
    for j = 3 to n-1
        if u[j].chain != stack.top().chain
            while stack.size() > 1
                connect(u[j], stack.pop())
            stack.push(u[j-1])
            stack.push(u[j])
        else
            last_popped = stack.pop()
            while !stack.empty()
                last_popped = stack.pop()
                if connect(last_popped, u[j]) != successful
                    break;
            stack.push(last_popped)
            stack.push(u[j])
    add diagonals from u[n] to all stack vertices except the first and the last

Theorem. a simple polygon with $n$ vertices can be triangulated in $\mathrm{O}(n\log n)$ time.

Point Location Query

2018.6.24, CGAA

Trapezoidal Map

问题: 给定一个包含$n$条边的planar subdivision $\mathcal{S}$和一个点$q$，求包含点$q$的$f\in \mathcal{S}$。

一种简单的做法是：过$\mathcal{S}$的每个顶点作一条平行于$y$轴的直线，于是这些直线把整个平面划分为了$\mathrm{O}(n)$个竖直条带，每个条带内部都不包含任何顶点。通过排序和二分查找，可以在$\mathrm{O}(n\log n)$时间内确定一个点位于哪个条带中；同时，每个条带至多被$n$条互不相交的边划分为$n+1$个区域，给定条带内一点，可以在$\mathrm{O}(n\log n)$时间内确定该点位于条带中的哪个区域中。这样一来，任给平面上一点，总能在$\mathrm{O}(n\log n)$时间内找出包含该点的面来。

这个算法的时间复杂度令人满意，却可能会占据$\mathrm{O}(n^2)$的额外空间，这对数据规模稍大的应用是不可接受的。

Non-crossing: 称两条平面线段是不相交的，当且仅当它们的交集为空或只包含自己的端点。

这里先引入一个预处理：用一个非常大的轴平行矩形$R$包含整个subdivision $\mathcal{S}$，任何待查询的点若落在该矩形区域外，都一律视为落在unbounded区域中。于是在接下来的处理中，可以假设待查询点一定落在某个有限大小的面中。同时，我们使用“将坐标轴微微旋转一个小角度”的trick，使得顶点的$x$坐标两两不相同。经预处理后的这组线段被称为是“in general position”的。

现考虑在$\mathcal{S}\cup R$的基础上，对每个顶点$v\in \mathcal{S}$，过$v$向上方和下方各投出一条射线（分别称为$v$的upper extension和lower extension），直到撞上$\mathcal{S}\cup R$中的其他线段为止。将经该步骤处理后的subdivision记为$\mathcal{T}(\mathcal{S})$。容易证明$\mathcal{T}(\mathcal{S})$中的所有面都是梯形或三角形，如果把三角形视为一条边长度为0的退化版梯形，就可以把$\mathcal{T}(\mathcal{S})$名正言顺地称作$\mathcal{S}$的“trapezoidal map”——

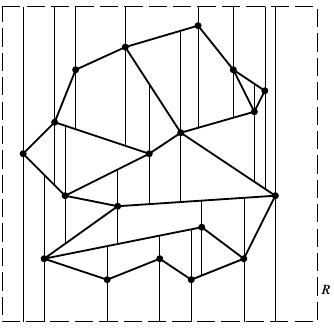
Lemma. Each face in a trapezoidal map of a set $\mathcal{S}$ of line segments in general position has one or two vertical sides and exactly two non-vertical sides.

Top & Bottom: 每个梯形$\Delta$一定有两个non-vertical sides，上面那个所对应的原$\mathcal{S}\cup R$中的边记作$\mathcal{T}(\Delta )$，下面那个对应的原$\mathcal{S}\cup R$中的边记作$\mathcal{B}(\Delta )$。

Left & Right: 除了整个$\mathcal{T}(\mathcal{S})$中最左侧和最右侧的两个矩形外，每个梯形$\Delta$左侧如果有条垂直边，那么记引出该垂直边的那个原$\mathcal{S}$中的顶点为$\mathcal{L}(\Delta )$，否则记$\mathcal{T}(\Delta )$和$\mathcal{B}(\Delta )$的唯一交点（位于$\Delta$的左侧）为$\mathcal{L}(\Delta )$。类似地，可以定义$\mathcal{R}(\Delta )$。

总而言之，一个梯形$\Delta$由它的上下边界线$\mathcal{T}(\Delta )$、$\mathcal{B}(\Delta )$和左右定界点$\mathcal{L}(\Delta )$、$\mathcal{R}(\Delta )$唯一地确定。

Lemma. the trapezoidal map $\mathcal{T}(\mathcal{S})$ of a set $\mathcal{S}$ of $n$ line segments in general position contains $\mathrm{O}(n)$ vertices and $\mathrm{O}(n)$ trapezoids.

Search Structure

这里给出一种数据结构$\mathcal{D}$，用来快速进行point location query的答复。$\mathcal{D}$是一个带根结点的有向无环图，对$\mathcal{T}(\mathcal{S})$中的每个梯形，$\mathcal{D}$中都有一个对应的叶结点。内部结点可分为$x$结点和$y$结点，出度均为2。每个$x$结点指向$\mathcal{S}$中某条线段的一个端点，每个$y$结点指向$\mathcal{S}$中的一条线段。

给定$\mathcal{D}$和待查询点$p$，从根结点开始，在每个内部结点处选择向左或向右移动，直到移动到一个叶结点为止。对$x$结点，按照$p$位于该结点中存储的顶点的左侧还是右侧进行选择；对$y$结点，按找$p$位于该结点中存储的线段上方还是下方进行选择。这里暂且假设不会发生$p_x$和$x$结点横坐标相等，或是$p$恰好落在$y$结点线段上的情况。下图是一个简单的$\mathcal{T}(\mathcal{S})$和它可能对应的$\mathcal{D}$：

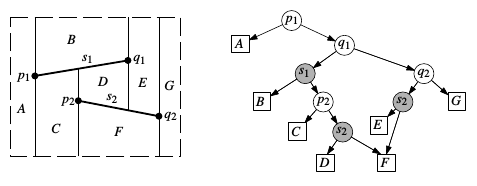
一般而言，以不同的顺序把元素插入一棵树中会影响到这棵树的结构，这里也不例外。在某些极端情况下，树搜索效率会退化得非常糟糕。这里给出一个随机算法，其运行时间和空间在期望意义上是令人满意的。

procedure trapezoidal_map(S: set of n non-crrssing line segments)
    make R
    init T as trapezoids of empty set
    init D with a single leaf node corresponding to R
    compute a random permutation s[1..n] of the segments in S
    for i = 1 to n
        find T[0..k] of trapezoids in T properly intersected by s[i]
        remove T[0..k] in T
        insert new trapezoids that appear because of the insertion of s[i] and T[0..k]
        remove leaves of T[0..k] in D
        create leaves for the new trapezoids
        link the new leaves to the existing inner nodes in D

设${\mathcal{S}}_i=\{s_1,\dots ,s_i\}$，则该算法的每轮循环结束时，$\mathcal{T}$始终是$\mathcal{T}({\mathcal{S}}_i)$，$\mathcal{D}$是$\mathcal{T}$的一个合法search structure。可以看出这是一个增量算法。

在从$\mathcal{T}({\mathcal{S}}_{i-1})$过渡到$\mathcal{T}({\mathcal{S}}_i)$时，某个梯形${\Delta }_j$不能被原样保留当且仅当$s_i$和${\Delta }_i$有交叉，因此循环体的第一步就是找出这些梯形T[1..k]（这里设T[1..k]按和$s_i$的相交位置从左往右排升序，显然T[j]和T[j+1]相邻）。跟据${\Delta }_j$很容易找出${\Delta }_{j+1}$，因此只需要找出${\Delta }_0$即可。而${\Delta }_0$就是$s_i$左端点所在的梯形（如果没有落在已有线段或顶点上的话），因此在现有的$\mathcal{D}$（恰为$\mathcal{T}({\mathcal{S}}_{i-1})$的search structure）上进行一次point location query就能找出${\Delta }_0$。

在查找${\Delta }_0$时，$s_i$的左端点$p$可能已经在${\mathcal{S}}_{i-1}$中的某条线段上，这时会出现沿着$\mathcal{D}$进行搜索时$p_x$和$x$结点横坐标相等，或是$p$恰落在$y$结点线段上的情况。这时，可以把$p$在概念上沿着$s_i$微微挪动向右到一个相邻的$p^{\prime }$。这样一来，对搜索时对$x$结点重合的情况，总是将$p$视为位于$x$结点的右侧；对恰好落在$y$结点的线段$s$上的情况，若$s$斜率大于$s_i$斜率，则认为$p$在$s$下方，反之上方。

综合前两段的讨论，寻找${\Delta }_0,\dots ,{\Delta }_k$即T[0..k]的算法为：

procedure find_Ts(T, D, s[i])
    let p = left end point of s[i]
    let q = right end point of s[i]
    search with p in the search structure D to find T[0]
    j = 0
    while q lies to the right of R(T[j])
        if R(T[j]) lies above s[i]
            let T[j+1] = lower right neighbor of T[j]
        else
            let T[j+1] = upper right neighbor of T[j]
        j = j + 1
    return T[0..j]

更新$\mathcal{T}$和$\mathcal{D}$的过程是复杂但平凡的，这里不再赘述。

Degenerate Cases

在之前的讨论中，算法略微旋转了坐标系，使得所有顶点的$x$坐标均无重合。由于实际计算机的计算精度相当有限，这一trick在实现上并不平凡。接下来，我们从理论上除去这一trick，方法是使用一个逻辑上的微量扭曲。对某个微小的$\epsilon >0$，构建如下顶点变换：

$$\phi :\left(\begin{array}{c}x\\ y\end{array}\right)\mapsto \left(\begin{array}{c}x+\epsilon y\\ y\end{array}\right)$$

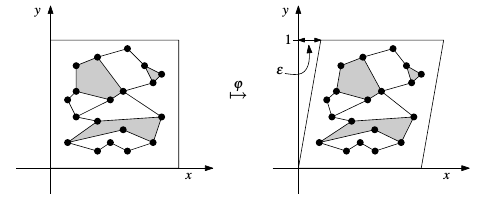
在接下来的运算中，实际使用的线段集合为$\phi \mathcal{S}=\{\phi s\mid s\in \mathcal{S}\}$。由于真正进行这一变换会遭遇数值计算上的困难，我们将$(x+\epsilon y,y)$记作$(x,y)$。在上面给出的算法中，我们从来没有计算过任何新的几何对象位置，而仅仅是使用本来就有的坐标，并对它们做一些比较或判断。因此，这一逻辑上的微量扭曲可以反映到涉及$x$坐标的判断操作上，使得任何两点的$x$坐标都不发生重合。

于是乎——

Theorem. algorithm trapezoidal_map computes the trapezoidal map $\mathcal{T}(\mathcal{S})$ of a set $\mathcal{S}$ of $n$ non-crossing line segments and a search structure $\mathcal{D}$ for $\mathcal{T}(\mathcal{S})$ om $\mathrm{O}(n\log n)$ time. The expected size of $\mathcal{D}$ is $\mathrm{O}(n)$ and for any query point $q$ the expected query time is $\mathrm{O}(n\log n)$.

期望时间的推导比较复杂，有闲心再看吧。

Voronoi Diagram

2018.6.24, CGAA

Definitions & Properties

Euclidean Distance: 平面上两点$p,q$间的欧氏距离定义为

$$\mathrm{dist}(p,q)=\sqrt{(p_x-q_x{)}^2+(p_y-q_y{)}^2}$$

Voronoi Diagram: 给定平面点集$P=\{p_1,\dots ,p_n\}$，$P$所定义的Voronoi Diagram（维诺图）是一个planar subdivision，每个face对应一个$p_i$。平面上一点$p$位于某个$p_i$的face内，当且仅当

$$\forall p_j\in P,p_j\ne p_i\Rightarrow \mathrm{dist}(p,p_i)<\mathrm{dist}(p,p_j)$$

将点集$P$确定的维诺图记为$\mathrm{Vor}(P)$。

Cell: $\mathcal{V}(p_i):={\bigcap }_{1\le j\le n,j\ne i}h(p_i,p_j)$，其中$h(p,q)$是以点$p,q$中线为边界的$p$那一边的半平面，即：

$$\mathcal{V}(p_i):=\bigcap _{1\le j\le n,j\ne i}\{r\mid \mathrm{dist}(r,p_i)<\mathrm{dist}(r,p_j)\}$$

Theorem. for $n\ge 3$, the number of vertices in the Voronoi diagram of a set of $n$ point sites in te plane is at most $2n-5$ and the number of edges is at most $3n-6$.

Cp: 定义$C_P(p)$为以$p\in {\mathbb{R}}^2$为中心的、内部不包含其他任何顶点的圆。显然$C_P(p)$是个闭集。

Theorem. 点$q\in {\mathbb{R}}^2$是$\mathrm{Vor}(P)$的一个顶点，当且仅当$C_P(q)$边界上有不少于3个$P$中的点。

Theorem. $p_i,p_j$连线的垂直平分直线的一个子线段是$\mathrm{Vor}(P)$的一条边，当且仅当存在点$q\in {\mathbb{R}}^2$使得$C_P(q)\cap P=\{p_i,p_j\}$

Computation

给定平面点集$P$，一种简单的计算其维诺图的方法是对每个$p_i\in P$，利用之前提到的布尔求交的方法计算$n-1$个半平面的交集，这将带来$\mathrm{O}(n^2\log n)$的时间复杂度，没什么用。接下来要介绍的是著名的Fortune算法，时间复杂度为$\mathrm{O}(n\log n)$。

Fortune算法也是基于sweep line的，它的框架和之前的线段求交算法有些相似——也有event point的概念。在sweep line $\ell$移动的过程中，要保证$\mathrm{Vor}(P)$在$\ell$上方的部分都已被计算出来是不现实的，这是由于这部分可能依赖于$\ell$下方的、还未被扫描到的点。Fortune退而求其次，维护任一时刻$\mathrm{Vor}(P)$在$\ell$上方、且和$\ell$下方顶点无关的部分。

首先我们需要一个标准——维诺图的哪部分一定不会受到$\ell$下方的点的影响？换言之，在$\ell$运动到某一位置时，设${\ell }^{+}$是$\ell$上方的半平面，哪些$q\in {\ell }^{+}$的$\arg {\min }_{p\in P}\mathrm{dist}(p,q)$是已知的？

容易注意到，$q$到$\ell$下方任何一个$p\in P$的距离都大于$q$到$\ell$的距离，因此，若

$$\mathrm{dist}(q,\ell )\ge \underset{p\in P\cap {\ell }^{+}}{\min }\mathrm{dist}(p,q)$$

则$q$在维诺图中的归属不可能和$\ell$下方的任何$p\in P$有关。可以证明，对每个$p\in P\cap {\ell }^{+}$，到$p$的距离小于到$\ell$的距离的点的边界是一条抛物线，于是我们有一系列这样的抛物线——

$${\beta }_{\ell }=\{{\beta }_p=\{q\mid \mathrm{dist}(p,q)=\mathrm{dist}(\ell ,q)\}\mid p\in P\cap {\ell }^{+}\}$$

称$\cup {\beta }_{\ell }$的下边界为beach line。Beach line由多条抛物线的一部分（arc）构成，beach line上各arcs的分界点称为break point（断点）。可以证明，随着$\ell$的移动，断点总是在$\mathrm{Vor}(P)$的边上移动。

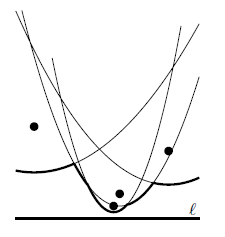
Observation. the beach line is $x$-monotone, that is, every vertical line intersects it in exactly one point.

Site事件: $\ell$在扫描过程中遇到一个$p\in P$，称为一个site事件。Site事件会产生两个新断点以及一个arc。事实上，这也是唯一能够产生新arc的情景——

Lemma. 一个新arc只可能在site事件中出现。

Circle事件: 对形成beach line上相邻的三段arc的的三个$P$中的点，称$\ell$和它们所确定的圆相切为一个circle事件。

Lemma. 一个已有的arc只可能在circle事件中消失。

其实有了site和circle事件的概念，我认为维诺图的算法就已经自然而然地出来了，只是这里有非常多的细节需要handle。需要注意的是：不是所有的arc都会在circle事件中消失；一些潜在的circle事件可能由于当事arc在别的circle事件中先消失而作废。

Theorem. the Voronoi diagram of a set of $n$ point sites in the plane can be computed with a sweep line algorithm in $\mathrm{O}(n\log n)$ time using $(n)$ storage.

Delaunay Triangulations

2018.6.25

Legal Triangulation

Triangulation: a triangulation of $P=\{p_1,\dots ,p_n\}\subset {\mathbb{R}}^2$ is a maximal planar subdivision whose vertex set is $P$.

Theorem. 设$P$中包含$n$个（不全共线的）顶点，其中有$k$个顶点位于构成$P$的凸包的多边形上，则$P$的任何三角化结果都包含$2n-n-k$个三角形，$3n-3-k$条边

Angle Vector: 任给点集$P$的一个三角化结果$\mathcal{T}$，若其中共包含$m$个三角形，则$m$个三角形共有$3m$个内角。这些内角非降序排列的结果$A(\mathcal{T}):=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{3m})$称为$\mathcal{T}$的角度向量。定义同一点集$P$的不同三角化结果的角度向量间的全序关系为角度的词法序。称$P$的三角化结果$\mathcal{T}$是角度最优的，当且仅当$A(\mathcal{T})$不小于任何其他$P$的三角化结果的角度向量。

Thale’s Theorem. 设直线$\ell$与圆$C$交于$a,b$两点，$p,q,r,s$落在$\ell$的同一侧。若$p,q$在$C$上，$r$在$C$内，$s$在$C$外，则$\angle arb>\angle apb=\angle aqb>\angle asb$。

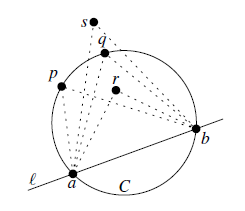
Edge Flipping: 在一个三角化结果$\mathcal{T}$中，任取一条非边界边$e$，$e$两边的两个三角形共同构成一个以$e$为对角线的四边形。将$e$替换为该四边形的另一条对角线后，将会得到另一个三角化结果${\mathcal{T}}^{\prime }$，这一替换操作称为一次edge flipping（边翻转）。边翻转会将两个三角形变为另外两个三角形。设翻转前两个三角形的六个内角为${\alpha }_1,\dots ,{\alpha }_6$，翻转后为${\alpha }_1^{\prime },\dots ,{\alpha }_6^{\prime }$，称$e$是一条非法边，当且仅当${\min }_i{\alpha }_i<{\min }_i{\alpha }_i^{\prime }$。

Theorem. 设$\mathcal{T}$包含非法边$e$，${\mathcal{T}}^{\prime }$是翻转$e$的结果，则$A({\mathcal{T}}^{\prime })>A(\mathcal{T})$。

这里有一个平凡的消去非法边的算法：

while there exists an illegal edge e
    flip e

由于在算法运行过程中，$A(\mathcal{T})$严格单调上升，因此该算法一定会停机，不过最坏效率就不敢恭维了。

Delaunay Triangulation

Delaunay Graph: 给定平面点集$P$，$\mathrm{Vor}(P)$的对偶图称为$P$的Delaunay Graph，记作$\mathcal{D}\mathcal{G}(P)$。

Theorem. Delaunary图总是可平面图。

General Position: 称一个点集是“in general position”的，当且仅当其中任意四个点都不在同一个圆上。这个概念用作点集的临时假设，可以简化算法叙述。

把按照Delaunay Graph连接顶点得到的三角化结果称为Delaunay三角化。