Hat Function

对一个有 $∣ V ∣$ 个顶点的三角形mesh，定义 $∣ V ∣$ 个对应的基函数，每个函数 $ϕ_{v}$ 和一个顶点 $v$ 对应。 $ϕ_{v}$ 的值由下式定义：

ϕ_{v} (v) ϕ_{v} (w) ϕ_{v} (p) := 1 := 0, := ϕ_{v} (i) B_{i} (p) + ϕ_{v} (j) B_{j} (p) + ϕ_{v} (k) B_{k} (p), w \in V - {v} p \in triangle ijk, p \in / V

其中 $B_{i} (p)$ 是点 $p$ 重心坐标（barycentric coordinate）的 $i$ 分量。简而言之， $ϕ_{v}$ 在顶点 $v$ 处为1，在其他顶点处为0，在非顶点处则按其所处三角形的重心坐标对三个顶点进行插值。

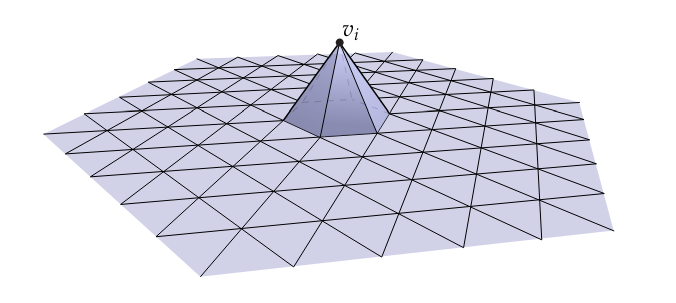center （图片来自CS 15-458/858: Discrete Differential Geometry. Keenan Crane）

我们可以用这些 $ϕ_{v}$ 的加权和来近似其他的复杂函数 $u$ ：

\overset{u}{^} = v \sum x_{v} ϕ_{v}

这就是“仅以顶点处的值构成的向量来表示整个函数”的几何解释。

Laplacian

Cotan Formula

给定triangle mesh $M$ 上的方程：

Δ u = f

显然：

\forall triangle D \in M, \forall v \in V, \int_{D} Δ u ϕ_{v} d A = \int_{D} f ϕ_{v} d A

此时根据green’s first identity，有：

\int_{D} Δ u ϕ_{v} d A = - \int_{D} \nabla u \cdot \nabla ϕ_{v} d A + \int_{\partial D} ϕ_{v} \nabla u \cdot n d l

假设我们的mesh是无边界的，那么对 $\partial D$ 的每条边，都一定有另一个三角形的一条边与之重合，且法线相反。因此，当我们同时考虑mesh $M$ 上所有的三角形时，上式右侧的第二项可以被抵消掉，只剩下：

\int_{M} Δ u ϕ_{v} d A = - \int_{M} \nabla u \cdot \nabla ϕ_{v} d A = - D \sum \int_{D} \nabla u \cdot \nabla ϕ_{v} d A

$u$ 可以被近似表示为 $\sum_{i} x_{i} ϕ_{i}$ ，于是：

\int_{M} Δ u ϕ_{v} d A = - D \sum \int_{D} \nabla (i \sum x_{i} ϕ_{i}) \cdot ϕ_{v} d A = - D \sum i \sum \int_{D} \nabla ϕ_{i} \cdot \nabla ϕ_{v} d A

注意到：

\int_{D} \nabla ϕ_{i} \cdot \nabla ϕ_{v} d A = ⎩ ⎨ ⎧ \frac{1}{2} (cot ⟨ \overline{ji}, \overline{jk} ⟩ + cot ⟨ \overline{ki}, \overline{kj} ⟩), - \frac{1}{2} cot ⟨ \overline{ji}, \overline{j v} ⟩, 0, i = v, D = ijk i \neq = v, D = ij v otherwise

从而：

\int_{M} Δ u ϕ_{v} d A = \frac{1}{2} i \in N (v) \sum (cot ⟨ \overline{ji}, \overline{j v} ⟩ + cot ⟨ \overline{ki}, \overline{k v} ⟩) (x_{i} - x_{v})

这就得到了著名的cotan公式。基于此，对每个顶点 $v$ ，都有：

\frac{1}{2} i \in N (v) \sum (cot ⟨ \overline{ji}, \overline{j v} ⟩ + cot ⟨ \overline{ki}, \overline{k v} ⟩) (x_{i} - x_{v}) = \int_{M} f ϕ_{v} d A

Area Matrix

注意我们对 $u$ 和 $f$ 的离散化方式并不相同， $u$ 被“分解”为一系列 $ϕ$ 的加权和， $f$ 则是被“投影”到了这些 $ϕ$ 上。这两种离散化都说得过去，如果想看看它们的关系，可以考虑将 $f$ 也表示为：

f = i \sum y_{i} ϕ_{i}

在与 $i$ 相邻的某个三角形 $ijk$ 中，容易证明：

\int_{D_{ijk}} f ϕ_{i} d A = A_{ijk} (\frac{1}{6} y_{i} + \frac{1}{12} y_{j} + \frac{1}{12} y_{k})

其中 $A_{ijk}$ 是三角形 $ijk$ 的面积。

如果用矩阵来表示 $y_{i}$ 和 $\int f ϕ_{i}$ 之间的关系，我们会发现它是对称的，但不是对角的。如果我们假定 $y_{i}, y_{j}, y_{k}$ 的差异很小，那么上面的积分结果可以被近似为 $(1/3) A_{ijk} y_{i}$ ，从而将其矩阵转换为对角阵——

A_{ii} = \frac{1}{3} triangle ijk \sum A_{ijk}

汇总

我们把cotan公式的矩阵表示记作 $L_{C}$ ，在实践中，常常把 $A^{- 1}$ 和 $L_{C}$ 预乘在一起，记作 $L = A^{- 1} L_{C}$ 。这样一来，原方程 $Δ u = f$ 被转换为了：

L x = y

可以证明 $L$ 是半正定的，十分便于求解。

Gradient

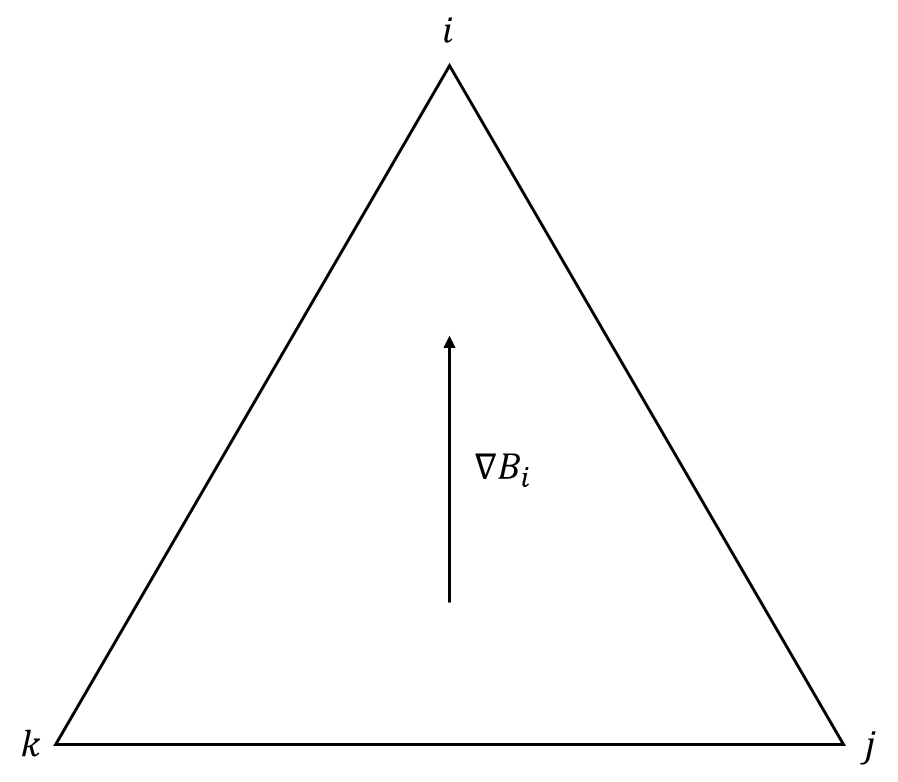
center

给定三角形 $ijk$ （ $i, j, k$ 以顺时针方向给出）各顶点的标量值 $u_{i}, u_{j}, u_{k}$ ，以重心坐标指定其内部每个点对应的 $u$ ：

u (p) = B_{i} (p) u_{i} + B_{j} (p) u_{j} + B_{k} (p) u_{k}

此时：

\nabla u = u_{i} \nabla B_{i} + u_{j} \nabla B_{j} + u_{k} \nabla B_{k}

接下来看看单独的 $\nabla B_{i}$ 。显然 $\nabla B_{i}$ 的方向是 $(p_{j} - p_{k})^{⊥}$ ， $⊥$ 表示将向量 $p_{j} - p_{k}$ 逆时针旋转90°，垂直于线段 $\overline{jk}$ 且朝向 $i$ 。此外， $B_{i}$ 在 $\overline{jk}$ 上为0，在 $i$ 处为1，故 $\nabla B_{i}$ 的大小为1除以 $i$ 到 $\overline{jk}$ 的距离——

∣\nabla B_{i} ∣ = \frac{∣ p _{j} - p _{k} ∣}{2 A _{ijk}}

其中 $A_{ijk}$ 是三角形 $ijk$ 的面积。

综合起来有：

\nabla u = u_{i} \nabla (1 - B_{j} - B_{k}) + u_{j} \nabla B_{j} + u_{k} \nabla B_{k} = (u_{j} - u_{i}) \nabla B_{j} + (u_{k} - u_{i}) \nabla B_{k} = (u_{j} - u_{i}) \frac{( p _{k} - p _{i} ) ^{⊥}}{2 A _{ijk}} + (u_{k} - u_{i}) \frac{( p _{i} - p _{j} ) ^{⊥}}{2 A _{ijk}}

Divergence

给定一个以三角形为单元的分段线性向量场 $X$ ，且 $X$ 的取值总是位于对应三角形所在的平面上（之前所讨论的梯度场就是一个绝佳的例子），来看看如何定义顶点处的散度。

center

考虑与顶点 $i$ 直接相连的一圈三角形，记其中的一个为 $ijk$ ，进行研究。设 $i$ 到 $jk$ 的距离为 $h$ ，取平行于 $\overline{jk}$ 、与 $i$ 相距 $h /2$ 的线段 $\overline{x y}$ 作为 $ijk$ 上的边界，则 $ijk$ 对 $i$ 的散度的贡献为：

\nabla_{ijk} \cdot X = ∣ p_{x} - p_{y} ∣ (X_{ijk} \cdot \frac{( p _{k} - p _{j} ) ^{⊥}}{∣ p _{k} - p _{j} ∣}) = \frac{1}{2} X \cdot (p_{k} - p_{j})^{⊥}

现记 $e_{1} = p_{j} - p_{i}, e_{2} = p_{k} - p_{i}$ ， $θ_{1}$ 为 $j$ 处的内角， $θ_{2}$ 为 $i$ 处的内角，考虑方程：

α e_{1} + β e_{2} = (p_{k} - p_{j})^{⊥}

将它分解到 $\overline{jk}$ 和 $\overline{jk}^{⊥}$ 这两个方向上：

α ∣ e_{1} ∣ cos θ_{1} α ∣ e_{1} ∣ sin θ_{1} + β ∣ e_{2} ∣ sin θ_{2} = β ∣ e_{2} ∣ cos θ_{2} = ∣ e_{1} ∣ cos θ_{1} + ∣ e_{2} ∣ cos θ_{2}

联立 $∣ e_{1} ∣ sin θ_{1} = ∣ e_{2} ∣ sin θ_{2}$ ，解得：

α = cot θ_{2} β = cot θ_{1}

因此 $ijk$ 对散度的贡献也可以写成：

\nabla_{ijk} \cdot X = \frac{1}{2} (e_{1} cot θ_{2} + e_{2} cot θ_{1}) \cdot X

遍历与 $i$ 相邻的所有三角形，将它们的上式值相加即可得到顶点 $i$ 的散度。

这里我们遗留了一个问题——为什么积分的边界被取作与 $i$ 相距 $h /2$ 的线段 $\overline{x y}$ ？这其实不是很有道理，因为和连续情形下的散度对不上。但如果从“ $laplace = div grad$ ”的角度出发，则可以给出一个解释。对包含顶点 $i$ 的一圈区域 $D$ 使用Stokes公式：

\int_{\partial D} X \cdot n d l = \int_{D} \nabla \cdot X d A

现假设 $X$ 是某个标量函数 $u$ 的梯度 $\nabla u$ ，则上式右侧是 $Δ u$ 在 $D$ 上的积分。此时，考虑上式在三角形 $ijk$ 中的部分：

\int_{\partial D} X \cdot n d l = \int_{\partial D} ((u_{j} - u_{i}) \frac{( p _{k} - p _{i} ) ^{⊥}}{2 A _{ijk}} + (u_{k} - u_{i}) \frac{( p _{i} - p _{j} ) ^{⊥}}{2 A _{ijk}}) \cdot n d l

如果把 $\partial D$ 取成三角形的中线，那么：

\int_{\partial D} X \cdot n d l = \frac{1}{4 A _{ijk}} ((u_{j} - u_{i}) (p_{k} - p_{i})^{⊥} \cdot (p_{k} - p_{j})^{⊥} + (u_{k} - u_{i}) (p_{i} - p_{j})^{⊥} \cdot (p_{k} - p_{j})^{⊥}) = \frac{1}{4 A _{ijk}} ((u_{j} - u_{i}) \overline{ki} \overline{kj} cos ⟨ \overline{ki}, \overline{kj} ⟩ + (u_{k} - u_{i}) \overline{ij} \overline{kj} cos ⟨ \overline{ji}, \overline{jk} ⟩) = \frac{1}{4 A _{ijk}} ((u_{j} - u_{i}) 2 A_{ijk} cot ⟨ \overline{ki}, \overline{kj} ⟩ + (u_{k} - u_{i}) 2 A_{ijk} cot ⟨ \overline{ji}, \overline{jk} ⟩) = \frac{1}{2} ((u_{j} - u_{i}) cot ⟨ \overline{ki}, \overline{kj} ⟩ + (u_{k} - u_{i}) cot ⟨ \overline{ji}, \overline{jk} ⟩)

由此可见，把 $\partial D$ 取成包含 $i$ 的一圈三角形的中线，就能使得“ $laplace = div grad$ ”成立。我们是在人为地构造梯度和cotan laplacian之间的桥梁，并把构造的结果称之为散度。

Automorphism

Discrete Differential Operators for Triangle Mesh