给一个triangle mesh $M$，以及上面的一组点$S$，求$M$上其他所有顶点到$S$的测地距离。

参考资料：The Heat Method for Distance Computation

本文代码：Rtrc Sample 15.HeatMethod

Heat Method

理论

如果以某个点$x$为热源在$M$表面做heat diffusion，将经过时间$t$后$y$点的热量记作$k_{t,x}(y)$，那么根据Varadhan’s formula，$k$和测地距离之间有如下关系：

$$\varphi (x,y)=\underset{t\to 0}{\lim }\sqrt{-4t\log k_{t,x}(y)}$$

换言之，我们可以用一个极短的时间步长模拟$M$上的热传输过程，然后用上式计算测地距离。然而当距离较大时，Varadhan’s formula会对数值精度提出不切实际的要求。因此这个做法仅在理论上正确，实践中没什么人用。

Keenan Crane大佬注意到：尽管$k$本身的数值精度不足以支撑Varadhan’s formula，但$k$的梯度方向仍然是相对准确的，而$\nabla k$的方向正好就是$\nabla \varphi$的方向。同时根据测地距离的定义，$|\nabla \varphi |=1$。因此，我们可以从$k$计算出$\nabla \varphi$，而从$\nabla \varphi$还原$\varphi$的过程就顺理成章了。

综上所述，可以用以下算法计算$\varphi$：

1. 选取一个较小的$t$，计算$k_{t,x}$
2. 计算$k_{t,x}$的梯度方向$\mathbf{X}=\nabla k_{t,x}/|\nabla k_{t,x}|$，这其实就是$\nabla \varphi$
3. 取$\mathbf{X}$的散度，解Poisson方程$\Delta \varphi =\nabla \cdot \mathbf{X}$，得到$\varphi$

这里细化第一步。Heat equation长这样：

$$\frac{\partial u}{\partial t}=\Delta u$$

取一个很小的时间步长，用backward Euler模拟一轮：

$$\frac{u_1-u_0}{t}=\Delta u_1$$

也就是：

$$(1-t\Delta )u_1=u_0$$

$u_0$是初始热源，$u_1$则是我们所需要的$k$。Triangle mesh上的$\Delta$算子可以参见我之前的博文Differential Operators for Triangle Mesh。

效果

我们在兔子上选一个点，首先模拟heat diffusion，得到$k$：

利用离散梯度算子把$k$转换成per-face的梯度并归一化，得到$\nabla \varphi$：

对$\nabla \varphi$求散度：

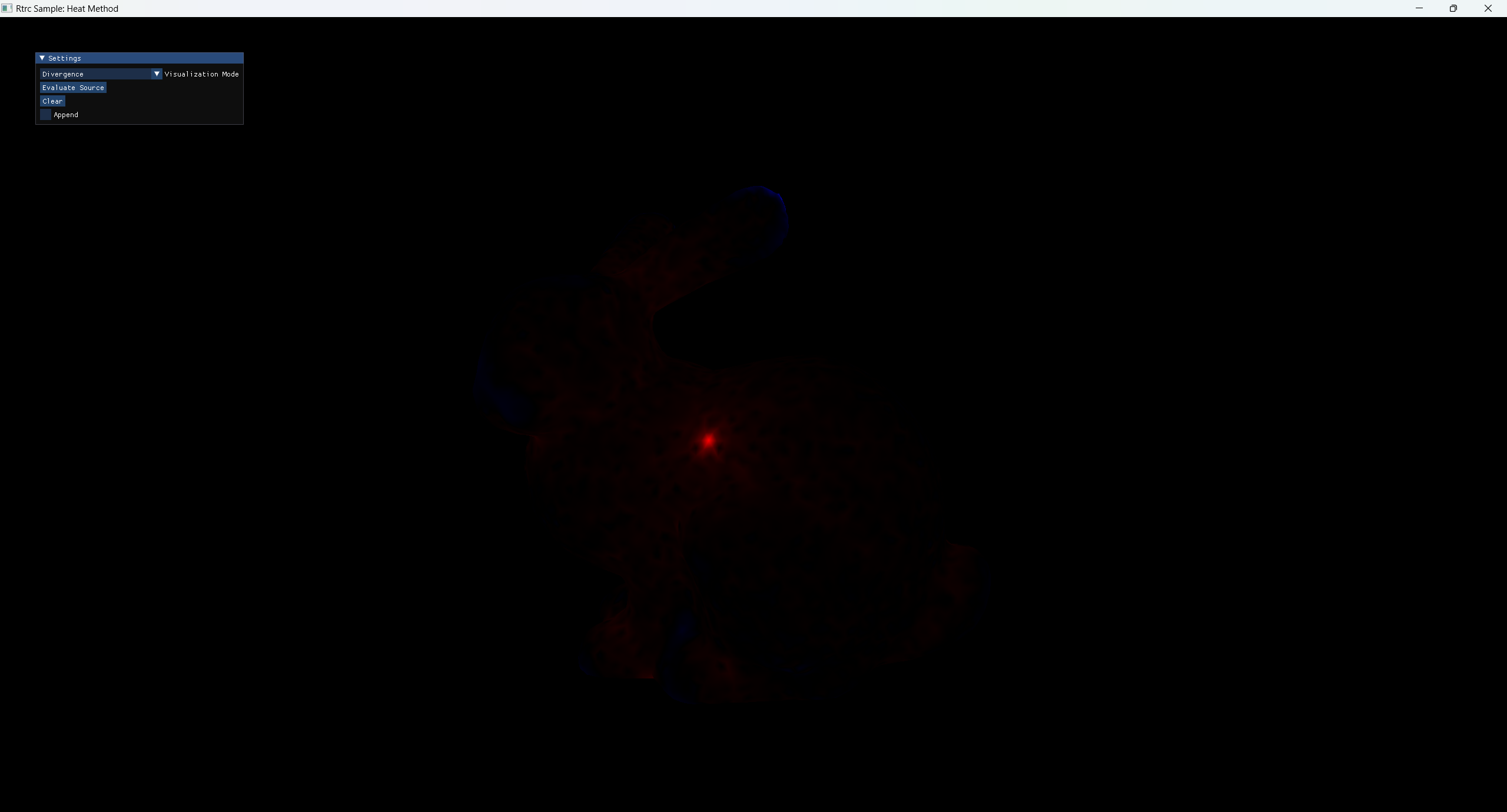
其中红色表示散度为正，蓝色为负。

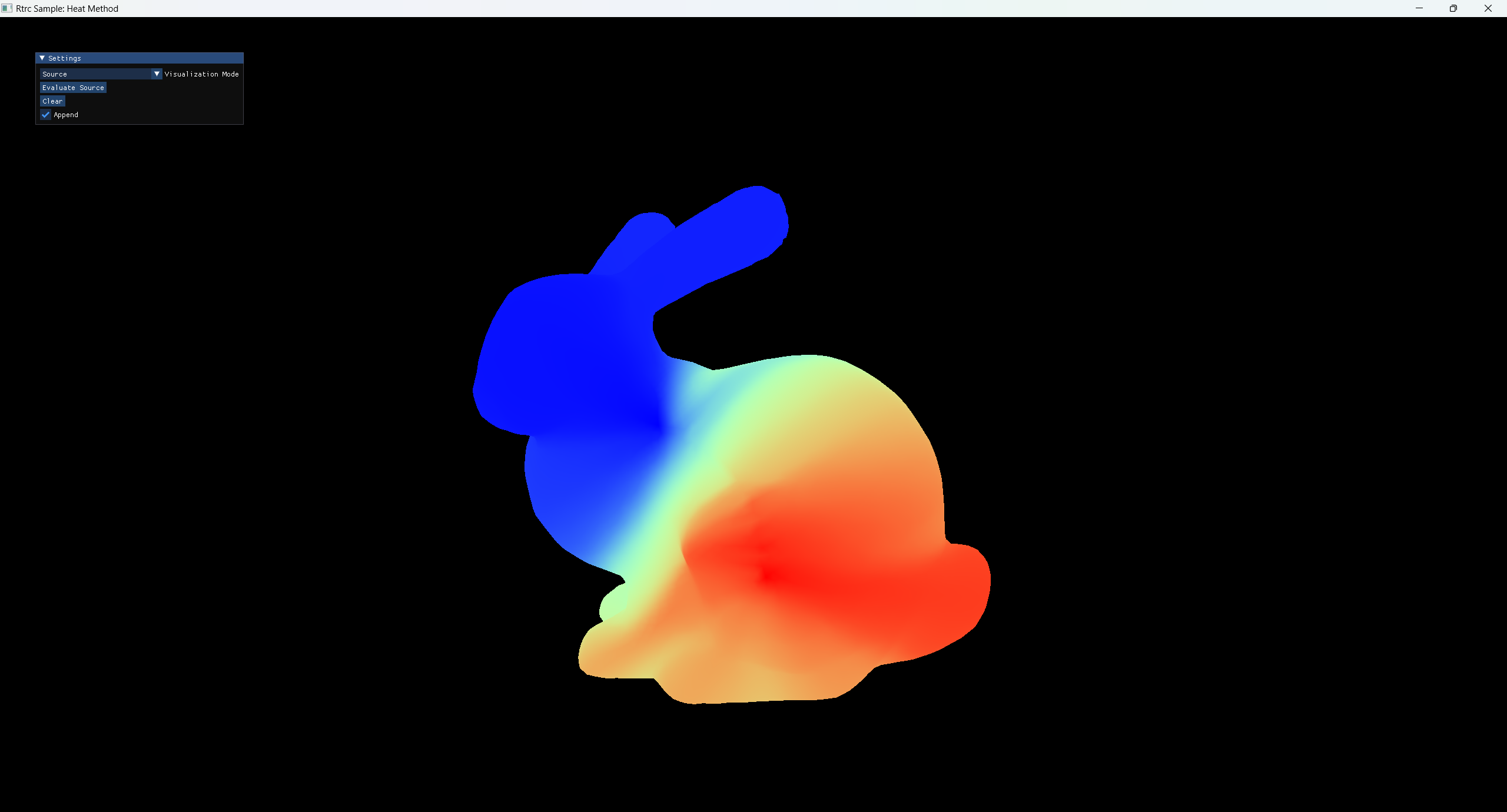
最后，解poisson方程得到$\varphi$，其分段可视化结果为：

这就得到了兔子上每一点到起始点的测地距离。

也可以选取多个源点，乃至连成线：

标量传输

当源点$S$不仅包含一个点，而是包含一条曲线、乃至一片区域时，我们可能不仅想知道其他点到$S$的测地距离，还想知道每个点和$S$中的哪个点最近。

换言之，如果给$S$中的每个点染个颜色，让这些颜色沿着测地线传播，那么我们想要求出mesh上每个位置最终的颜色。

首先，让我们给每个源点设定初始值：

$$u_i=\text{predefined value for }i,i\in S$$

$u$沿着测地线传输，也就是说它在测地线方向上不会发生变化——

$$\nabla u\cdot \nabla \varphi =0$$

在实践中，我们对每个三角形$D$，都可以从未知量$u$构建$D$上的$\nabla u$；而$D$上的$\nabla \varphi$是之前的heat method中已经计算过的。这样一来，我们就获得了方程数量等同于三角形数量的线性方程组，构成关于$u$的稀疏线性系统。

在$|S|>1$时，triangle mesh中的面数不会少于未知顶点数，再加上在各种离散化和数值误差，我们的线性方程组可以被看成是overdetermined。此时，可以用最小二乘法得到一组合理的$u$值。

我们把上面那条曲线形状的$S$的左上端染成蓝色，右下端染成红色，中间插个值，然后让颜色沿着测地线传输，得到的结果如下：

而如果把这里的$S$做个arc-length parameterzation，把结果沿着测地线传播出去，然后将测地距离和传播结果分别作为UV的两个通道可视化出来，就能得到下面的结果：

如果我们只关注离$S$较近的区域，那么这应该是个不错的局部参数化方法，拓展版的DEM。